Chapter 4: Mechanism of Scientific Change

Intro

So far, we have given a number of examples of how both accepted theories and methods of theory evaluation have changed through time. These changes portray scientific mosaics as dynamic and seemingly always in flux. So, you might be wondering: is there some underlying universal mechanism that governs the changes in theories and methods that we see in scientific mosaics? Or is it the case that theories and methods change in a completely random fashion, without exhibiting any general patterns? To answer that question, we have to first tackle the broader philosophical question of whether a general theory of scientific change is possible at all. Doing so will require making a number of clarifications from the outset.

When we consider any particular science, there are two relatively distinct sets of questions that we can ask: particular questions and general questions. Particular questions ask about specific events, data points, phenomena, or objects within a certain science’s domain. Particular questions in a field like ornithology (the study of birds) might be:

Is that blue jay a male or a female?

How many eggs did that snowy owl lay this season?

Did the Canada geese begin flying south late this year?

In contrast, general questions ask about regular patterns, or about classes of events, phenomena, or objects in a certain science’s domain. General questions in ornithology (corresponding with the particular questions above) might be:

What are the physical or morphological differences between male and female blue jays?

What environmental factors affect snowy owl egg production?

What are the typical migration patterns of Canada geese?

Often, answers to particular questions are relatively straightforward theories:

The blue jay in question is a male.

The owl laid a clutch of 3 eggs.

The Canada geese left late.

But interestingly, these questions often depend upon answers to the general questions we asked above. In order to determine whether the blue jay is male or female, for instance, the ornithologist would have to consult a more general theory about typical morphological sex differences in blue jays. The most apt general theories seem to emerge as answers to general questions from within a specific scientific domain.

Now, it is possible – and sometimes necessary – to draw from the general theories of other sciences in order to answer particular questions. For instance, if we did not yet have a general theory for determining the sex of a blue jay, we might rely upon general theories about sexual difference from generic vertebrate biology. That said, while helpful, general theories from related disciplines are often vague and more difficult to apply when one is trying to answer a very specific, particular question.

The question “Can there be a general theory of scientific change?” is therefore asking whether we can, in fact, unearth some general patterns about the elements of science and scientific change – the scientific mosaic, theories, methods, etc. – and whether it’s possible to come up with a general theory about them, on their own terms. We can clearly ask particular questions about different communities, their mosaics, and changes in them:

What different scientific communities existed in Paris ca. 1720?

What version of Aristotelian natural philosophy was accepted in Cambridge around 1600?

What method did General Relativity satisfy to become accepted?

Yet, we can also ask general questions about the process of scientific change, such as:

What is the mechanism by which theories are accepted?

What is the mechanism of method employment?

But are we in a position to answer these general questions and, thus, produce a general theory of scientific change? Or are particular questions about scientific change answerable by general theories from other fields, like anthropology or sociology?

Generalism vs. Particularism

Let’s frame the debate with two opposing conceptions, which we will call generalism and particularism: does the process of changes in theories and methods exhibit certain general patterns? Answering “yes” to this question would make one a supporter of the conception we’ve called generalism. Generalists believe that there is some sort of an underlying mechanism that governs transitions from one theory to the next and one method to the next and, therefore, a general theory of scientific change is possible, in principle. To answer “no” to this question would make one a supporter of what we’ve called particularism. Particularists believe that there can be no general theory of scientific change.

It should be noted at the outset that there is no communal consensus among historians and philosophers of science regarding the issue of particularism vs. generalism. That said, particularism, not generalism, has more widespread acceptance among individual historians and philosophers of science nowadays. They take this position for a number of reasons, four of which we will unpack below.

Argument from bad track record: There have been a number of attempts to fashion theories that could answer general questions about scientific change. Despite the fact that some of these theories were accepted by individual historians and philosophers of science, none have ever become accepted by the community of historians and philosophers of science. While these theories were often ingenious, one of their principal drawbacks has been their failure to account for the most up-to-date knowledge from the history of science. Consider, for instance, Karl Popper’s conception of scientific change, according to which the process of scientific change is essentially a series of bold conjectures and decisive refutations. In this Popperian picture of science, a theory is accepted only provisionally as the best available hypothesis and is immediately rejected once we observe an anomaly, i.e. something that goes against the predictions of the theory. However, historical studies show that scientific communities often exhibit remarkable tolerance towards anomalies. For example, in 1859, it was discovered that the observed orbit of the planet Mercury deviates slightly from the one predicted by the then-accepted Newtonian theory. This was clearly an anomaly for the accepted theory and if science functioned according to Popper’s dicta, the Newtonian theory would have to be rejected. Yet, it is a historical fact that the Newtonian theory remained accepted for another 60 years until it was replaced by general relativity ca. 1920.

These historical failings are explained slightly more thoroughly in points 2 and 3 below. The “argument from bad track record” considers these failed attempts all at once. In short, every general theory of scientific change suggested so far has been left unaccepted. The conclusion of the argument, therefore, is an inductive inference: since every attempt to craft a general theory has ended up unaccepted, it seems likely that no general theory will ever be accepted. This argument isn’t the strongest, since it makes a rather pessimistic inference drawn from very little data, but it is an argument against generalism nonetheless.

Argument from Changeability of Scientific Method: Previous attempts to propose a general theory of scientific change tried to ground those theories in a single set of implicit expectations and requirements which all scientific communities had shared throughout history. That is, philosophers of science like Carnap, Popper, Lakatos and others between the 1920s and the 1970s tried to explicate a single method of science common to all scientific communities, past, present, and future. If we figure out what that method is – they reasoned – we can point to a set of unchanging requirements or expectations to help us answer the general question “how do new scientific theories get accepted?”

But as we know from chapter 3, a more careful historical analysis reveals that there has been no single, transhistorical or transdisciplinary method of science. Scientific methods, in fact, do change through time. If answers to general questions about scientific change depend upon a static method of science, and the method of science is dynamic, then when faced with the question “Can there be a general theory of scientific change?” we would seem compelled to respond “no”.

Argument from Nothing Permanent: One can take this line of reasoning from the changeability of the scientific method a step further. The efforts of historians of science have demonstrated that reconstructing the theories and methods held by any scientific community involves also accounting for an incredibly complex set of social, political, and other factors. For instance, to even begin to reconstruct the theories and methods of the scientific community of the Abbasid caliphate, which existed on the Arabian peninsula between 750–1258 C.E., a historian must be familiar with that particular society’s language, authority structure, and what types of texts would hold the accepted theories of that time. All of these would be starkly different from the factors at play in Medieval Europe during the same period! This is all to say that in addition to showing that there are diverse scientific methods across geography and time, it seems that almost anything can vary between scientific communities. Across time and space, there might be nothing permanent or fixed about scientific communities, their theories, or their methods.

The claim here is that, because neither methods nor nearly anything else can ground patterns of change at the level of the mosaics of scientific communities, there’s no way that we could have a general theory of scientific change, nor general answers to the general questions we might ask about it. Those who marshal this argument therefore eschew any general approach to science and instead focus on answering particular questions about science: questions about the uniqueness and complexity of particular scientific communities or transitions within particular times and places. Often, these historical accounts will be communicated as a focused story or narrative, giving an exposition of a particular historical episode without relying on any general theory of scientific change.

Argument from Social Construction: While historical narratives might be able to avoid invoking or relying upon a general theory of scientific change, they cannot avoid relying upon general theories of some sort. Even the most focused historical narratives invoke general theories in order to make sense of the causes, effects, or relationships within those episodes. It is accepted by historians that Queen Elizabeth I cared deeply for Mary, Queen of Scots. The traditional explanation for this is that they were cousins. Clearly this explanation is based on a tacit assumption, such as “cousins normally care for each other”, or “relatives normally care for each other”, or even “cousins in Elizabethan England cared for each other”, etc. Regardless of what the actual assumption is, we can appreciate that it is a general proposition. Such general propositions are an integral part of any narrative.

For a large swath of contemporary historians, the constitution and dynamics of the scientific mosaic can be explained by referencing the general theories of sociology and anthropology. In other words, the patterns and regularities needed to have such general theories can be found in the way that communities behave, and how individuals relate to those communities. Since there are good arguments for why scientific change lacks these patterns, and since there is no accepted general theory that identifies and explains them, many philosophers and historians of science see the dynamics of scientific theories and methods as social constructs, and thus best explained by the best general theories of sociology and anthropology. So, the argument from “social construction” is slightly more nuanced than the arguments that have come before it. It claims that particular changes in science can be best explained with general theories from sciences like sociology and anthropology, not general theories of scientific change which have typically failed to capture the nuances of history. In short, many philosophers and historians are doubtful about the prospects of a general theory of scientific change.

But what if there were a general theory which offered rebuttals to all four of the previously mentioned arguments for particularism? What if there were a general theory of scientific change which could accommodate the nuances and complexities of historical-geographic contexts, and also managed to recognize and articulate constant features in the historical dynamics of scientific mosaics?

The remainder of this chapter is dedicated to introducing a general theory of scientific change which proposes four laws which can be said to govern the changes in the scientific mosaic of any community. This general theory has formed the centrepiece of a new empirical science called scientonomy, where it is currently accepted as the best available description of the process of scientific change. However, note that from the viewpoint of the larger community of historians, philosophers, and sociologists of science this theory is not currently accepted but merely pursued. In the process of explaining this new general theory of scientific change, we will labour to demonstrate how this general theory rebuts all of the major arguments used to support particularism. Hopefully it will become clear by the end of the chapter why the development and refinement of this theory is worth pursuing, and perhaps even why we might be able to answer “yes” to the question “can there be a general theory of scientific change?”

Method Employment

To begin, let’s do a thought experiment based on the history of medical drug testing. Suppose that you and a group of other scientists want to determine whether a certain medicine can help people with insomnia fall asleep more easily. Let’s call the medicine you’d like to test Falazleep. What you are ultimately doing is seeing whether the theory “Falazleep helps individuals with insomnia fall asleep” is acceptable to the scientific community or not.

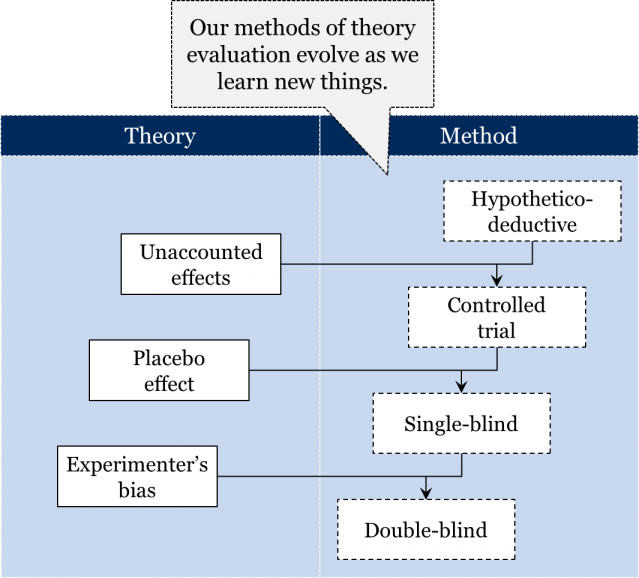
One of the most straightforward ways of seeing whether Falazleep can help individuals go to sleep more easily is to simply give the proper dose of Falazleep to people who suffer from insomnia. If some of those people report being able to sleep more easily, then it seems reasonable for the scientific community to accept the theory that Falazleep is therapeutically effective, i.e. that it works, at least in certain cases. What we’ve articulated here is a very basic version of the hypothetico-deductive (HD) method: in order to accept this causal relationship between Falazleep and sleep, you have to confirm your theory’s prediction that, when given to insomniacs, Falazleep will indeed help them sleep.

You and your peers give a group of insomniacs Falazleep and, sure enough, many of them do in fact fall asleep more easily. Having confirmed your theory’s prediction, you and the scientific community accept the theory that Falazleep helps individuals with insomnia fall asleep.

A few years later, you and your peers are asked to test a new drug, Falazleep Z. However, the scientific community has come to the realization that other factors – such as the recipients’ exercise, diet, stress level, and so forth – could have actually been the cause of the reported easier sleep in your previous trial, not Falazleep itself. That is, you and the scientific community now accept the theory of unaccounted effects, which says “factors other than the medication may influence the outcome of a medical drug test study.” Knowing what you know now, can you and your peers test Falazleep Z the same way you tested the original Falazleep? No!

Why not? Because now you and the rest of the scientific community accept that your earlier test – simply giving Falazleep to insomniacs – didn’t even begin to distinguish between the effects of Falazleep and the other variations in the test subjects’ lives. In order for your new test results to be accepted, you have to meet the scientific community’s new expectation: that you find a way to distinguish between the effects of Falazleep Z and other variations in the test subjects’ lives.

So, you and your colleagues take a large group of insomniacs and split them in two groups, each of which you study for the duration of the trial. However, only one group – the so-called “active group” – actually receives Falazleep Z. The other group, which we will label the “control group”, receives no medication. At the end of the trial, if the active group’s improvement with Falazleep Z is significantly greater than the improvement in the control group, then perhaps the scientific community will accept that Falazleep Z is therapeutically effective. This is especially likely because the experimental setup, today called a “controlled trial,” accounts for previously unaccounted effects, such as the body’s natural healing ability, improved weather, diet, and so on.

A few more years go by, and you and your peers are asked to test another drug, Falazleep Zz. But in the meantime, it has been found that medical drug trial participants can sometimes show drastic signs of improvement simply because they believe they are receiving medication, even if they are only being given a fake or substitute (candy, saline solution, sugar pills, etc.). In other words, the scientific community accepted a theory that belief in effective treatment might actually produce beneficial effects, called the placebo effect. Perhaps some of the efficacy of the Falazleep Z trial from a few years back was because some participants in the active group believed they were getting effective medicine…whether the medicine was effective or not!

So, in your trial for Falazleep Zz, you need to now account for this newly discovered placebo effect. To that end, you and your peers decide to give both your active group and your control group pills. However, you only give Falazleep Zz to the active group, while giving the control group sugar pills, i.e. placebos. Importantly, only you (the researchers) know which of the two groups are actually receiving Falazleep Zz. Because both groups are receiving pills, but neither group knows whether they’re receiving the actual medicine, this experimental setup is called a blind trial. Now suppose the improvement in the condition of the patients in the active group is noticeably greater than that of the patients in the control group. As a result, the scientific community accepts that Falazleep Zz is therapeutically efficient.

Another few years pass, and you and your group test the brand-new drug FASTazleep. Since your last trials with Falazleep Zz, the scientific community has discovered that researchers distributing those pills to the control and active groups can give off subtle, unintended cues as to which pills are genuine and which are fake. Unsurprisingly this phenomenon, called experimenter’s bias, prompts test subjects in the active group who have picked up on these cues to improve, regardless of the efficacy of the medication. Because you and your peers accept this theory of experimenter’s bias, you know the scientific community expects a new theory to account for this bias. Consequently, you devise a setup in which neither those administering the pills nor those receiving the pills actually know who is receiving FASTazleep and who is receiving a placebo. In other words, you perform what is nowadays called a double-blind trial.

Hopefully this repetitive example hasn’t put you “FASTazleep”! The repetition was purposeful, it was meant to help elucidate the pattern found not only in the actual history of drug trial testing, but in the employment of new methods in science generally. As you may have noticed, when the scientific community accepted a new theory – say, the existence of the placebo effect – their implicit expectations about what would make a new theory acceptable also changed. Remember, we’ve called these implicit expectations and requirements of a scientific community their method. Thus, we can conclude that changes in our criteria of theory evaluation, i.e. in our methods, were due to changes in our accepted theories:

That new accepted theories cause employed methods to change is the fundamental insight which is the essence of a law of scientific change, which we’ve called the law of method employment. According to the law of method employment, a method becomes employed only when it is deducible from some subset of other employed methods and accepted theories of the time:

This law captures a pattern, a regularity that occurs time and again in the history of science when a community comes to employ a new method. Indeed, it seems to successfully describe the mechanism of both minor changes in employed methods, such as any of the examples from medical drug trial testing above, and even more substantial changes in employed method, such as the shift from the Aristotelian-Medieval (AM) to the hypothetico-deductive (HD) method. Importantly, the third law describes not only that new methods are shaped by new theories, but how those methods are shaped by those theories. As you can see in the formulation of the law, a new method is employed only if that method is a deductive consequence of, i.e. if it logically follows from, some other theories and methods which are part of that scientific community’s mosaic.

Now that we know the mechanism of transitions from one method to the next, we can appreciate why methods are changeable. In chapter 3 we provided a historical argument for the dynamic method thesis by showing how methods of theory evaluation were different in different historical periods. Now we have an additional – theoretical – argument for the dynamic method thesis. On the one hand, we know from the third law that our employed methods are deductive consequences of our accepted theories. On the other hand, as fallibilists, we realize that our empirical theories can change through time. From these two premises, it follows that all methods that assume at least one empirical theory are, in principle, changeable.

This law also helps us cast light on what features of historical mosaics led to the employment of certain methods at certain times. Consider for instance the assumptions underlying the hypothetico-deductive method. It is safe to say that the HD method is a deductive consequence of very specific assumptions about the world.

One such assumption is the idea of complexity, according to which the world, as it appears in observations, is a product of some more fundamental inner mechanism. This assumption has been tacitly or explicitly accepted since the early 18th century. It is because of this assumption that we tolerate hypotheses about the existence of unobservable entities, such as elementary particles, waves, forces, etc. The reason why we tolerate such hypotheses is that we accept the possibility that there might be entities and relations that are not directly observable. In other words, we believe that there is more to the world than meets the eye. We wouldn’t tolerate any hypotheses about unobservables if we believed that the world is composed only of immediately observable entities, properties, relations, etc.

The second assumption underlying the HD method is the idea that any phenomenon can be given many different post hoc explanations which are equally precise. We’ve already witnessed this phenomenon. Recall, for example, different theories attempting to explain free fall, ranging from the Aristotelian “descend towards the centre of the universe” to the general relativistic “inertial motion in a curved space-time”. But since an explanation of a phenomenon can be easily cooked up after the fact, how do we know if it’s any good? This is where the requirement of confirmed novel predictions enters the picture. It is the scientists’ way of ensuring that they don’t end up accepting rubbish explanations, but only those which have managed to predict something hitherto unobserved. A theory’s ability to predict something previously unobserved is valued highly precisely due to the risk of post hoc explanations. Indeed, novel predictions wouldn’t be necessary if there were no risk of cooked up post hoc explanations.

In short, just like the drug testing methods, the HD method too is shaped by our knowledge about the world.

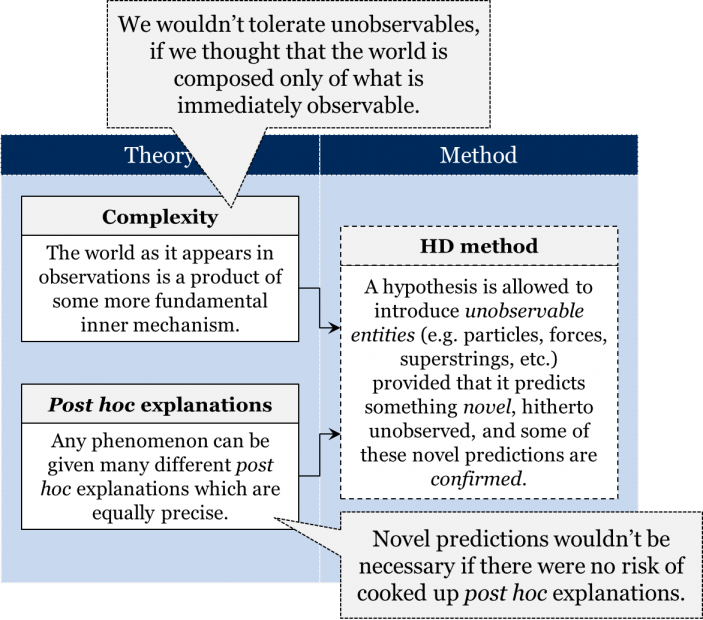
It is important to appreciate that the HD method is also changeable due to the fact that the assumptions on which it is based – those of complexity and post hoc explanations – are themselves changeable.

The same goes for the Aristotelian-medieval method – it was also shaped by the theories accepted at the time. One of the assumptions underlying the AM method is the idea that every natural thing has its nature, an indispensable (substantial) quality that makes a thing what it is. For instance, what makes an acorn an acorn is its capacity to grow into an oak tree. Similarly, the nature of a lion cub is its capacity to grow into a full-fledged lion. Finally, according to this way of thinking, the substantial quality of a human being is the capacity of reason.

The second assumption underlying the AM method is the idea that the nature of a thing can be grasped intuitively by an experienced person. In a nutshell, the idea was that you get to better understand a thing as you gain more experience with it. Consider a beekeeper who has spent a lifetime among bees. It was assumed that this beekeeper is perfectly positioned to inform us on the nature of bees. The same goes for an experienced teacher who, by virtue of having spent years educating students, would know a thing or two about the nature of the human mind.

The requirements of the AM method deductively follow from these assumptions. The Aristotelian-medieval scholars wouldn’t expect intuitive truths grasped by an experienced person if they didn’t believe that the nature of a thing can be grasped intuitively by experienced people or if they questioned the very existence of a thing’s nature.

Once again, we see how a community’s method of theory evaluation is shaped by the theories accepted by that community.

It is important to understand that a method can be composed of criteria of three different types – acceptance criteria, demarcation criteria, and compatibility criteria. So far, when talking about methods, we have focused on acceptance criteria. These are the criteria that determine whether a theory is acceptable or unacceptable. However, there are at least two other types of criteria. Demarcation criteria determine whether a theory is scientific or unscientific, while compatibility criteria determine whether two theories are compatible or incompatible within a given mosaic.

Since the third law of scientific change applies to all methods, it applies equally to all three types of criteria. While, so far, our historical examples concerned changes in acceptance criteria, the third law also explains how demarcation criteria and compatibility criteria change through time. Below we will discuss some examples of different compatibility criteria and how they are shaped by accepted theories. As for different demarcation criteria, we will discuss them in chapter 6.

To re-emphasize a point made earlier, we claim that this same mechanism of method employment is at work in any historical period, in any scientific community. In science, methods and any criteria they contain are always employed the same way: our knowledge about the world shapes our expectations concerning new theories. But this is not the only transhistorical feature of scientific mosaics and their dynamics. The law of method employment is only one of four laws that together constitute a general theory of scientific change. Let’s look at the remaining three laws in turn.

Theory Acceptance

As we’ve just seen, a mosaic’s method is profoundly shaped by its accepted theories, and methods will often change when new theories are accepted. But how does a scientific community accept those new theories? As with method employment, there seems to be a similarly universal pattern throughout the history of science whenever new theories are accepted into a mosaic.

Whether you’ve noticed it or not we have given you many examples of the mechanism of theory acceptance in action. We saw how Fresnel’s wave theory of light was accepted ca. 1820, how Einstein’s theory of general relativity was accepted ca. 1920, and how other theories like Mayer’s lunar theory and Coulomb’s inverse square law were all accepted by their respective scientific communities. In chapter 3 we also considered the case of Galileo, which was a scenario in which the scientific community did not accept a proposed new theory. So, what was not the case in the Galileo scenario that was the case in every other scenario we have just mentioned? In the case of Galileo, his heliocentric theory did not satisfy the method of the time. Every other theory which became accepted did satisfy the method of their respective communities at the time of assessment.

Indeed, in every situation we’ve considered where a new contender theory is eventually accepted into a mosaic, the theory is only accepted if it somehow meets the requirements of that scientific community’s method. To perhaps oversimplify this finding slightly: a theory is only accepted when a scientific community judges that it is acceptable! One of our earlier versions of the law of theory acceptance was actually very similar to this insight, saying that in order to become accepted into the mosaic, a theory is assessed by the method actually employed at the time. This did the trick for a while, but we came to realize that it only tells us that to be accepted a theory must be assessed, but that it doesn’t tell us the conditions that actually lead to its acceptance. For that reason, we have reformulated the law in a way that, while slightly less elegant, clearly links the theory’s assessment by the method to the possible assessment outcomes:

So, if a theory satisfies a mosaic’s employed method, it is accepted. If a theory fails to satisfy the employed method – if it fails to meet the implicit expectations of that community – it will simply remain unaccepted and will not become part of the mosaic. If it is unclear whether the method has been satisfied or not (“assessment is inconclusive”), the law simply describes the two logically possible outcomes (accepted or not accepted). Most importantly for our purposes, however, are the two clear-cut scenarios: when a theory is assessed by the method of the time, satisfaction of the method always leads to the theory’s acceptance, and failure to satisfy the method always leads to the theory remaining unaccepted.

It is important to remember that there is not one universal scientific method that has been employed throughout history, so the requirements that a theory must satisfy in order to be accepted will depend on the method of that particular community at that particular time. Yes, this means that a theory being assessed by the method of one mosaic might be accepted, and a theory assessed by the method of a different mosaic might remain unaccepted. But methods are not employed willy-nilly, and their requirements are not chosen randomly! Despite the fact that both theories and methods change, these changes seem to follow a stable pattern, which we’ve captured in the two laws we’ve discussed thus far. The exciting diversity and variety in science is not the sign of an underlying anarchism or irrationality, but seems to be the result of stable, predictable laws of scientific change playing out in the rich history of human discovery and creativity.

The laws of method employment and theory acceptance are laws which focus on the way that the elements of mosaics change, and how new elements enter into the mosaic. But while change may be inevitable, we also know that science often displays periods of relative stability. So, is there a standard way in which theories and methods behave when there are no new elements being considered?

Scientific Inertia

When Isaac Newton presented his laws of motion in his 1687 opus Philosophiæ Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy), his obvious focus was on the dynamics of moving bodies and their influence on one another. But he realized that even objects which were not noticeably interacting with one another were also part of his physical system and should therefore be described as well. Newton’s first law of motion about physical objects therefore answered the question: What happens when something is not being acted upon? His answer was that such an object basically continues doing what it was doing: if it was moving, it continues moving at the same rate in a straight line. If it was at rest, it remains at rest. He called this law his law of inertia – the Latin word inertia means “inactivity.”

What happens when the elements in our mosaic are not being “acted upon”? If there’s no new theory being accepted, or no new method being employed, how do the existing elements of the mosaic behave? It seems that elements in a scientific mosaic maintain their place in that mosaic: that is, if a theory had been accepted, that theory continues to be accepted; if a method had been employed, it continues to be employed. Due to this coincidental similarity between Newton’s first law of motion and the historical behaviour of the elements of scientific mosaics in times of relative stability, we have called this law of scientific change the law of scientific inertia. As precisely formulated, the law of scientific inertia states that an element of the mosaic remains in the mosaic unless replaced by other elements:

There are two major implications of this law that we need to unpack.

First, recall that if a theory is in a mosaic, it’s an accepted theory, and if a method is part of a mosaic, it’s an employed method. That is, if an element is part of the scientific mosaic, it has already been “vetted” by the community. What scientific inertia entails, therefore, is that these same theories are never re-assessed by the method, nor are these methods’ requirements re-deduced. The integration of a particular element into the mosaic happens once (for theories, with the mechanism of theory acceptance; for methods, method employment) and it remains part of the mosaic until it’s replaced by another element.

Second, replacement is essential to understanding this law properly. An element never just “falls out” of a mosaic; it has to be replaced by something. This is most clear in the case of theories, since even the negation of an accepted theory is itself a theory and can only be accepted by satisfying the method of the time. For instance, suppose that a scientific community’s accepted theory changes from “the moon is made of cheese,” to “the moon is not made of cheese.” Is this an example of a theory simply disappearing from the mosaic? No. The negation of a theory is still a theory! Presumably the theory “the moon is not made of cheese” satisfied the method of the time and was accepted as the best available description of the material makeup of the moon, thereby replacing the earlier cheese theory.

What does scientific inertia look like in the real world? In biology today, the accepted theory of evolution is known as the modern synthesis; it has been accepted since the middle of the twentieth century. Two central sub-theories of the modern synthesis are “evolution results from changes in gene frequencies in populations of organisms,” and “populations adapt to their environments by natural selection.” Within the last 30 years or so, even strong proponents of the modern synthesis have begun to agree that these two sub-theories are inadequate, and that the modern synthesis struggles to account for well-known biological phenomena (such as epigenetics, niche construction, and phenotypic plasticity). Despite this building dissatisfaction, however, the modern synthesis remains the accepted theory in contemporary biology. Why? It is because no contender theory has yet satisfied the method of the biology community, as per the law of theory acceptance. Until a new theory can be proposed that satisfies the method of the biology community – and therefore replace the modern synthesis – the modern synthesis will remain the “best available” theory of evolution.

Compatibility

The fourth and final law of scientific change describes the scientific mosaic at any moment of time and is known as the law of compatibility. The law of compatibility states that at any moment of time, the elements of the scientific mosaic are compatible with each other:

If two or more elements can exist in the same mosaic, we say that they are compatible with one another. If two or more elements cannot exist in the same mosaic, we say those elements are incompatible. This law simply points out that in any one scientific mosaic, all elements – theories and methods – are judged to be compatible.

The notion of compatibility must not be confused with the logical notion of consistency. Two theories are said to be logically consistent when there is no contradiction between them. Compatibility is the ability of theories to coexist within a community’s mosaic regardless of their mutual consistency or inconsistency. Thus, in principle, it is possible for two logically inconsistent theories to be nevertheless compatible within a community’s mosaic. In other words, compatibility is a relative notion: the same pair of theories may be compatible in one mosaic and incompatible in another.

What, ultimately, arbitrates which theories and methods are compatible with one another? In other words, where can we find the implicit requirements (i.e. expectations, criteria) which the scientific community would have for what is compatible and what is not? You guessed it: the method of the time. What is compatible in a mosaic, therefore, is determined by (and is part of) the method of the time, specifically its compatibility criteria. Just like any other criteria, compatibility criteria can also differ across different communities and time periods. Thus, a pair of theories may be considered compatible in one mosaic but incompatible in another, depending on the compatibility criteria of each mosaic.

But how do these compatibility criteria become employed? They become employed the same way any other method becomes employed: as per the law of method employment, each criterion is a deductive consequence of other accepted theories and employed methods. Let’s look at some examples of different compatibility criteria and how they become employed.

Recall that in the formal sciences we can make claims of absolute knowledge, because any formal proposition is simply a definition or follows from definitions. Communities in formal sciences, therefore, would employ an infallibilist method and consider a theory acceptable only if it is demonstratively true. We also know from the logical law of noncontradiction that contradictory propositions cannot both be true at the same time. Since accepted propositions in formal sciences are considered demonstratively true, it deductively follows that two theories which contradict each other cannot possibly be accepted at the same time in the mosaic of the same formal science community, since only one of them can be demonstratively true. This explains why formal science communities are normally intolerant towards inconsistencies. If we assume that the contemporary formal science community accepts that their theories are absolutely true, it follows deductively that in the mosaic of this formal science community, all logically inconsistent theories are also necessarily incompatible. Thus, this community would be intolerant towards inconsistencies, i.e. for this community inconsistent theories would be incompatible:

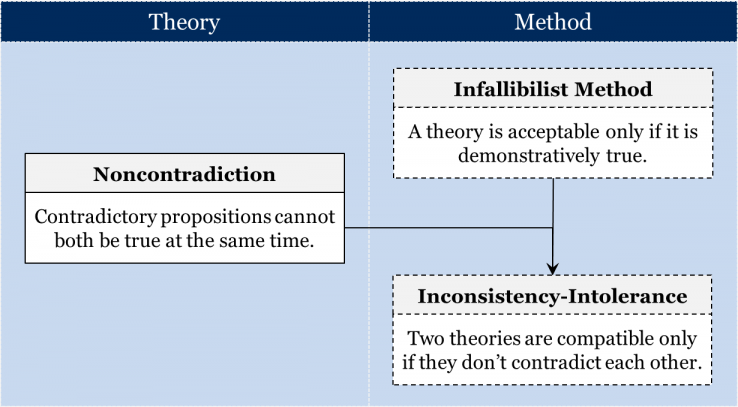
This is therefore a main facet of the compatibility criteria of this community’s method. If this scientific community were to accept a new theory that was inconsistent with any earlier theories, those earlier theories would be considered incompatible and therefore rejected from the mosaic.

But are there communities that are tolerant towards inconsistencies? That is, does inconsistency always entail incompatibility? The short answer is “no”. Let’s consider the mosaic of an empirical science like contemporary physics. The contemporary physics community accepts both quantum mechanics and general relativity as part of their mosaic. Quantum mechanics deals principally with incredibly small objects, like the elements of the standard model (quarks, leptons, and bosons), while general relativity deals with incredibly large-scale objects and high energy interactions, like the bending of space by massive objects and velocities approximating the speed of light. But, interestingly, these two theories are inconsistent with one another when it comes to their interpretation of an object that belongs to both of their domains, such as the singularity within a black hole. It belongs to both domains because singularities are incredibly small and thus should be covered by quantum physics, yet they also have an incredibly large mass and thus should be covered by general relativity. When the two theories are simultaneously applied to singularities, the inconsistency between the two becomes apparent. And yet these two inconsistent theories are simultaneously accepted nowadays and are therefore considered to be compatible despite this inconsistency. Why might that be the case?

Remember that the contemporary physics community (like all empirical science communities) is fallibilist, so it is prepared to accept theories that are far from being demonstratively true. This community is content to accept the best available approximations. (Look back at chapter 2 if you need a refresher as to why!) In addition, this empirical science community also accepts that contradictory propositions can both be approximately (or quasi-) true. If theories cannot be absolutely true, then it is at least possible that two obviously inconsistent theories might still nevertheless be considered – in certain circumstances – compatible. In this case, physicists realize that they have two incredibly successful theories that have independently satisfied the employed HD method, but that these two theories focus on different scales of the physical universe: the tiny, and the massive, respectively. Their fallibilism and the two distinct domains carved out by each branch of physics lead us to conclude that physicists are tolerant towards inconsistencies:

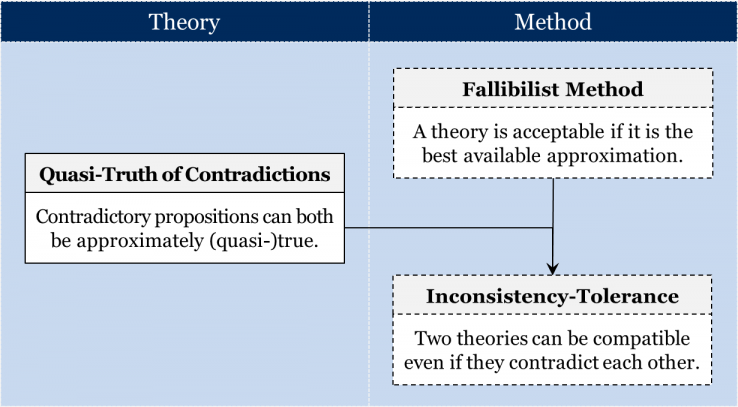
Naturally, an empirical science community need not necessarily be tolerant towards all inconsistencies. For instance, it may limit its inconsistency toleration only to accepting inconsistent theories that belong to two sufficiently different domains. For example, an empirical science community can be tolerant towards inconsistencies between two accepted theories when each of these theory deals with a very distinct scale. Alternatively, it may only be tolerant towards inconsistencies between an accepted theory and some of the available data obtained in experiments and observations. In any event, it shouldn’t be tolerant towards all possible inconsistencies to qualify as inconsistency-tolerant.

The Four Laws of Scientific Change

We have now introduced you to all four laws of scientific change. But we didn’t introduce you to them in numerical order! The typical ordering of the laws is this:

Scientific inertia was given the honour of being the first law, as something of an homage to Newton’s laws of motion (as explained above). The law of compatibility has been called the zeroth law precisely because it is a “static” law, describing the state of the mosaic during and between transitions. For the purposes of this textbook, it is important to learn the numbers of each respective law, since the numbers will act as a helpful shorthand moving forward. For instance, we can simply reference “the third law” instead of writing about “the law of method employment”.

These four laws of scientific change together constitute a general theory of scientific change that we will use to help explain and understand episodes from the history of science, as well as certain philosophical topics such as scientific progress (chapter 5) and the so-called demarcation problem (chapter 6). The laws serve as axioms in an axiomatic-deductive system, and considering certain laws together helps us shed even more light on the process of scientific change than if we only consider the laws on their own. In an axiomatic-deductive system, propositions deduced from axioms are called theorems. Currently, over twenty theorems have been deduced from the laws of scientific change, but we will only briefly consider three.

Some Theorems

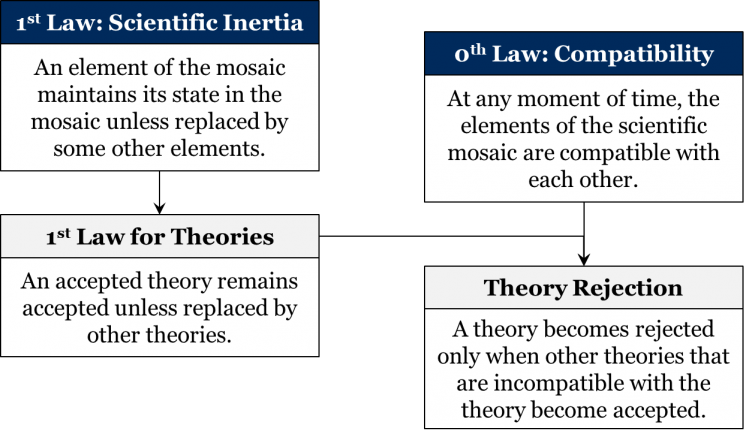
We’ve talked about how theories are accepted, but can we be more explicit about how they are rejected? If we look at the first and zeroth laws together we can derive the theory rejection theorem. By the first law, an accepted theory will remain accepted until it is replaced by other theories. By the zeroth law, the elements of the scientific mosaic are always compatible with one another. Thus, if a newly accepted theory is incompatible with any previously accepted theories, those older theories leave the mosaic and become rejected, and are replaced by the new theory. This way compatibility is maintained (according to the zeroth law) and the previously accepted theories are replaced by the new theory (according to the first law).

How do new theories become appraised? Specifically, is it at all possible to evaluate a theory in isolation from other theories? For a long time, it was believed by philosophers that the task of theory evaluation is to take the theory and determine whether it is absolutely true or false. If a theory passes the evaluation, then it is considered absolutely true; if not, it is considered false. This is the gist of the conception of absolute theory appraisal, according to which it is possible to assess a standalone theory without comparing it to any other theory. However, this conception of absolute appraisal would only make sense if we were to believe that there is such a thing as absolute certainty. What happens to the notion of theory appraisal once we appreciate that all empirical theories are fallible? When philosophers realized that no empirical theory can be shown to be absolutely true, they came to appreciate that the best we can do is to compare competing theories with the goal of establishing which among competing theories is better. Thus, they arrived at what can be called the conception of comparative theory appraisal. On this view of theory appraisal, any instance of theory evaluation is an attempt to compare a theory with its available competitors, and therefore, theory appraisal is never absolute. In other words, according to comparative theory appraisal, there is no such thing as an appraisal of an individual theory independent of other theories.

In recent decades, it has gradually transpired that while all theory appraisal is comparative, it is also necessarily contextual, as it depends crucially on the content of the mosaic in which the appraisal takes place. Specifically, it is accepted by many philosophers and historians these days that the outcome of a theory’s appraisal will depend on the specific method employed by the community making the appraisal. Thus, it is conceivable that when comparing two competing theories, one community may prefer one theory while another may prefer the other, depending on their respective employed methods. We can call this view contextual theory appraisal. Importantly, it is this view of theory appraisal that follows from the laws of scientific change.

Considering the first and second laws, we can derive the contextual appraisal theorem. By the first law, a theory already in the mosaic stays in the mosaic insofar as it is not replaced by other theories. This means that once a theory is accepted into the mosaic, it is no longer expected to satisfy any requirements to stay in the mosaic. By the second law, a theory is assessed by the method employed at the time of the assessment. In other words, the assessment takes place when members of a community attempt to bring a theory into the mosaic. As such, theory assessment is an assessment of a proposed modification of the mosaic by the method employed at the time. In other words, theory assessment is contextual as it takes place within a particular historical/geographical context, by that particular scientific community’s method.

What happens when two incompatible theories satisfy the community’s employed method at the same time? By the second law, we know that if a theory satisfies the method of the time, it will be accepted. From the zeroth law, however, we know that all elements in a mosaic are compatible with one another. So, if two incompatible theories simultaneously satisfy the same employed method, to maintain compatibility the mosaic itself splits: you would have one entirely compatible mosaic containing one theory as accepted, and a second entirely compatible mosaic containing the other. This is known as the mosaic split theorem.

There are many examples of mosaic split in the history of science, the most famous of which occurred between the Newtonian and Cartesian mosaics at the turn of the 18th century. Up until this point the scientific community throughout Europe employed the Aristotelian-Medieval method. You’ll recall that the acceptance criteria for the AM method required that the theory be intuitive to an experienced person. Isaac Newton’s vast axiomatic-deductive system of physical theorems was derived from his three simple laws of motion and his law of universal gravitation. René Descartes’ equally impressive axiomatic-deductive system (incompatible with that of Newton) was similarly deduced from a set of intuitively obvious axioms, such as “Matter is extension.” Faced with these two impressively comprehensive sets of theories, the scientific community found that both satisfied their (vague) AM acceptance criterion of being “intuitive”: both systems began from easily-graspable axioms and validly deduced a plethora of theorems concerning different aspects of the physical world from them. The result was that both theories became accepted, but that the mosaic itself split in two: one Newtonian, one Cartesian.

But what historical factors decide who becomes Newtonian and who becomes Cartesian? The mosaic split theorem tells us that, given the circumstances, a split is going to take place. Yet, it doesn’t say which part of a previously unified community is going to accept Newtonianism and which part is going to accept Cartesianism. From the perspective of the laws of scientific change, there is nothing determining which of the two new communities will accept what. It’s reasonable to suspect that a variety of sociocultural factors play a role in this process. Some sociological explanations point to the fact that France, home to Descartes, and Britain, home to Newton, were rival nations celebrating and endorsing the discoveries and advancements of their own people first. Other explanations pointing to the theological differences between the mosaics of France and Britain from before 1700, with Catholicism accepted in the former and Anglicanism in the latter. Keep in mind that in early modern Europe, theological propositions and natural philosophical propositions were typically part of the same mosaic and had to be compatible with one another. In such a case, the acceptance of Cartesianism and Newtonianism in France and the Continent respectively represented the widening rather than beginning of a mosaic split. We will have an opportunity to look at these two mosaics (and explore exactly why they were incompatible) in the history chapters of this textbook.

Summary

Can there be a general theory of scientific change? To begin answering the question we first made a distinction between general and particular questions, and between general and particular theories. We went on to clarify that generalists answer “yes” to this question, and that particularists answer “no.” Afterwards we introduced four arguments used to support particularism. However, we went on to argue for generalism, and presented the four laws of scientific change as a promising candidate for a general theory of scientific change. By way of review, let’s see how we might respond to the four main arguments for particularism via the laws of scientific change.

Bad Track Record: While poor past performance of general theories of scientific change is indeed an argument against generalism, it doesn’t rule out the possibility of the creation of a new theory that has learned from past mistakes. The laws of scientific change take seriously history, context, and change, and seem to succeed where other theories have failed. It’s a contender, at least!

Nothing Permanent (Including the Scientific Method): Combining the second and third arguments, particularists note that stability and patterns are the cornerstone for answering general questions with general theories, and “science” doesn’t seem to have them. With no fixed method and with highly unique historical contexts, the prospect for grounding a general theory seems nearly impossible. The laws of scientific change, however, are not grounded in some transhistorical element of a mosaic. Rather, they recognize that the way science changes, the patterns of scientific change, are what remain permanent throughout history. The four laws are descriptions of the stable process by which theories and methods change through time. Besides this, the laws, in their current form, don’t ignore the uniqueness and peculiarities of certain historical periods. The laws rather incorporate them into science’s transhistorical dynamic (see the contextual appraisal & mosaic split theorems).

Social Construction: In the absence of a general theory of scientific change, some historians have attempted to explain individual scientific changes by means of the theories of sociology and anthropology. But hopefully our exposition of the laws has, at least, helped to demonstrate that the process of scientific change has its own unique patterns that are worth studying and describing on their own terms. Indeed, the laws show that not only can general questions be asked about science, but general answers seem to be discoverable as well. Using general theories from a related discipline can be helpful, but why stick with more vague theories that are harder to apply when more specific theories are at your fingertips?

While particularism remains the currently accepted position in this debate, it is clearly unjustified, as all of its main arguments are flawed:

We will pursue and use the laws of scientific change throughout the remainder of this textbook. As fallibilists, we realize that the laws of scientific change are imperfect and will likely be improved. But we are confident that the laws of scientific change as they stand now are at least a valuable tool for parsing the sometimes overwhelmingly complex history of science.